Transformed Outcome

Let’s redefine target variable, which indicates that treatment make some impact on target or did target is negative without treatment:

\[Z = Y * \frac{(W - p)}{(p * (1 - p))}\]

• \(Y\) - target vector,

• \(W\) - vector of binary communication flags, and

• \(p\) is a propensity score (the probabilty that each \(y_i\) is assigned to the treatment group.).

It is important to note here that it is possible to estimate \(p\) as the proportion of objects with \(W = 1\) in the sample. Or use the method from [2], in which it is proposed to evaluate math:p as a function of \(X\) by training the classifier on the available data \(X = x\), and taking the communication flag vector math:W as the target variable.

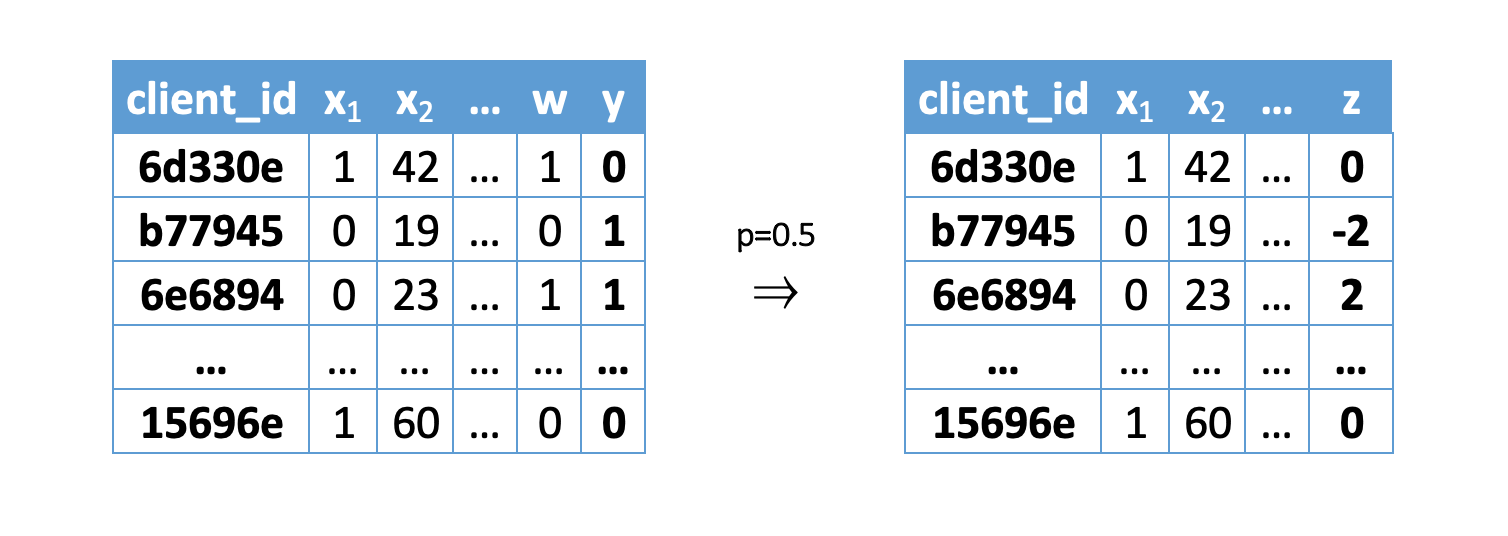
After applying the formula, we get a new target variable \(Z_i\) and can train a regression model with the error functional \(MSE= \frac{1}{n}\sum_{i=0}^{n} (Z_i - \hat{Z_i})^2\). Since it is precisely when using MSE that the predictions of the model are the conditional mathematical expectation of the target variable.

It can be proved that the conditional expectation of the transformed target \(Z_i\) is the desired causal effect:

\[E[Z_i| X_i = x] = Y_i^1 - Y_i^0 = \tau_i\]

Hint

In sklift this approach corresponds to the ClassTransformationReg class.

References

1️⃣ Susan Athey and Guido W Imbens. Machine learning methods for estimating heterogeneouscausal effects. stat, 1050:5, 2015.

2️⃣ P. Richard Hahn, Jared S. Murray, and Carlos Carvalho. Bayesian regression tree models for causal inference: regularization, confounding, and heterogeneous effects. 2019.